Example 1 In the integral we may write = , = , = , so that the integral becomes = = ( ) = = = = , provided For a definite integral, the bounds change once the substitution is performed and are determined using the equation = , with values in the range <©05 BE Shapiro Page 3 This document may not be reproduced, posted or published without permission The copyright holder makes no representation about the accuracy, correctness, orThe slope of the tangent line is the value of the derivative at the point of tangency;

Mastering Olympiad Mathematics Math Joke Square Root
Sqrt(1+tan^2 c) joke meaning
Sqrt(1+tan^2 c) joke meaning-Mathematics √x = sqrt(x) In C Programming The sqrt() function is defined in mathh header file To find the square root of int , float or long double data types, you can explicitly convert the type to double using cast operatorLevel 2 1 point · 7 years ago "Baby you are 1/cos(c)" You either use the moment of confusion to make a run for it, or you're in


Math Pick Up Lines Pick Up Lines
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreBecause even though the equationArithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
C did not support function overloading That means that there had to be one different function for each type Hence a sqrt for double and sqrtf for floatSince double was the "preferred" type for floating point numbers in C, then the "default" version was the one for doubleBoth are part of the C standard library, in mathh In C, the overloaded sqrt (defined in cmath, in namespace stdMar 01, 18 · `=sqrt((1cos a)^2/(sin^2a))` We then find the square root `=(1cos a)/(sin a)` Of course, we would need to make allowance for positive and negative signs, depending on the quadrant in question We can also write the tangent of a half angle as follows `tan (alpha/2)=(sin alpha)/(1cos alpha)`Jul 29, 14 · Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation History
The normal line is a line that is perpendicular to the tangent line and passes through the point of tangencyChapter 4 Trigonometry Emphasize the value and importance of making sketches, where appropriate It is very important for learners to understand that it is incorrect to apply the distributive law to the trigonometric ratios of compound angles and that \(\cos (\alpha \beta) \ne \cos \alpha \cos \beta\)) So this is not really an equation (if it were, it would be meaningless) But if you consider each element separately you discover that this is a riddle or code for a certain word Let me explain



What Are Some Funny Mathematics Jokes Quora


Maths Jokes
View more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator LearnYou have already been told about the useful identity $$1\tan^2 x=\frac{1}{\cos^2 x}$$ You may have seen this identity as $$1\tan^2x =\sec^2 x$$ There are slightly tricky things about taking square roots, but they are not a problem in the interval where you are working We end up wanting to find $\int \sec x dx$, or equivalently $\int dxWe don't need the square root of math1/math Complex numbers can certainly be defined without math\sqrt{1}/math Indeed, in order to explain to their fellow mathematicians (and to themselves) that complex numbers are not just hogwash but


Funny Short Math Jokes And Puns Math Is Fun



Maths Jokes
In this video I calculate an antiderivative of the square root of 1x^2 using trigonometric substitution (and the triangle method) and along the way I also cSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep



What Is The Funniest Math Joke You Know Of Beakal Tiliksew Brilliant



Mastering Olympiad Mathematics Math Joke Square Root
Mar 21, · In this interval, $(\tan x 1)$ is positive but $(\tan x\sqrt{3})$ is negative, meaning the final result is negative and hence $\lt 0$ So here's your final answer $\dfrac{\pi}{4}2\pi n \lt x \lt \dfrac{\pi}{3}2\pi n \quad n \in \mathbb{N}$Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorJan 12, 17 · Using #cos^2 x sin^2 x = 1# #tan x = sin x / cos x# #sec x = 1/cos x# we find #sqrt(1tan^2 x) = sqrt(1(sin^2 x)/(cos^2 x))# #color(white)(sqrt(1tan^2 x


Trig Insert Clever Math Pun Here



I M 1 Tan C And I Know It Mathpics Mathjoke Mathmeme Pic Joke Math Meme Haha Funny Humor Pun Lol Trigonometry Algebra2 Tshirt Tangent Secant Squareroot Funny Meme On Me Me
Thanks for the A Are you referring to this?Integrate 1/(cos(x)2) from 0 to 2pi;Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor



Mathematics For The Ib Diploma Analysis And Approaches Sl Draft Copy By Hodder Education Issuu


Math Pick Up Lines Pick Up Lines
Examples The square root of the area of a square represents the length of any side of the square The following example displays the area of some cities in the United States and gives an impression of each city's size if it were represented by a squareCalculating the mean, median, mode, and range of a data set is a fundamental part of learning statistics Use this video to practice your skills and then test your knowledge with a short quizApr 26, 21 · Trigonometry Formulas Trigonometry is the branch of mathematics that deals with the relationship between the sides and angles of a triangle There are many interesting applications of Trigonometry that one can try out in their daytoday lives For example, if you are on the terrace of a tall building of known height and you see a post box on the other side of the road, you can



Music A Mathematical Offering Dave Benson University Of Aberdeen


Diary Outline For Math 152h Fall 09
Nov 08, 19 · In C#, MathSqrt() is a Math class method which is used to calculate the square root of the specified number Sqrt is a slower computation It can be cached for a performance boost Syntax public static double Sqrt(double d) Parameter d Number whose square root is to be calculated and type of this parameter is SystemDouble Return Type This method returns theLearn how to find the approximate values of square roots The examples used in this video are √32, √55, and √123 The technique used is to compare the squares of whole numbers to the number we're taking the square root ofFeb 09, · I was studying Prof Padmanabhan's book on general relativity;



What Is The Funniest Math Joke You Know Of Beakal Tiliksew Brilliant


What Is The Funniest Math Joke You Know Of Beakal Tiliksew Brilliant
In your mathematical careers you might encounter people who say it is wrong to say that I is equal to the principal square root of negative one and if you ask them why is this wrong they'll show up with this this kind of line of logic that actually seems pretty reasonable they will tell you that okay well let's just start with negative one we know from definition that negative one is equal toApr 02, 14 · One Day day a constant function f(x)=c and f(x)=e(pow,x) was roaming together Suddenly they both saw that a differential operator d/d() was approaching the constant function freaked out of fear and left the place very quickly the f(x)=e(pow, x) was smiling to see that fear, and he said to himself, d/d(x) can do nothing to meIntegrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;



Mathematics Narinder



If Tan 8 2 3 What Is Sin 8 Quora
Solving Equations Involving a Single Trigonometric Function When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and the unit circleCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history10 The point represented by $2 i$ in the Argand plane moves $1$ unit eastwards, then $2$ units northwards and finally from there $2 \sqrt{2}$ units in the southwestwards direction



10 Extra Cheesy Math Jokes Explained The Enotes Blog



Funny Short Math Jokes And Puns Math Is Fun
The following proof is very similar to one given by Raifaizen By the Pythagorean theorem we have b 2 = h 2 d 2 and a 2 = h 2 (c − d) 2 according to the figure at the right Subtracting these yields a 2 − b 2 = c 2 − 2cdThis equation allows us to express d in terms of the sides of the triangle = For the height of the triangle we have that h 2 = b 2 − d 2By replacing d withType in 2/sqrt(2) (=) Function Reference A function will return NaN (Not a Number) when you give it invalid entries, such as sqrt(1) Operators Addition operator Subtraction operator * Multiplication operator / Division operator ^"Gravitation Foundations and Frontiers, which I found very well written I just started the book and the exercises are also challengi



Sci Jokes Pdfcoffee Com
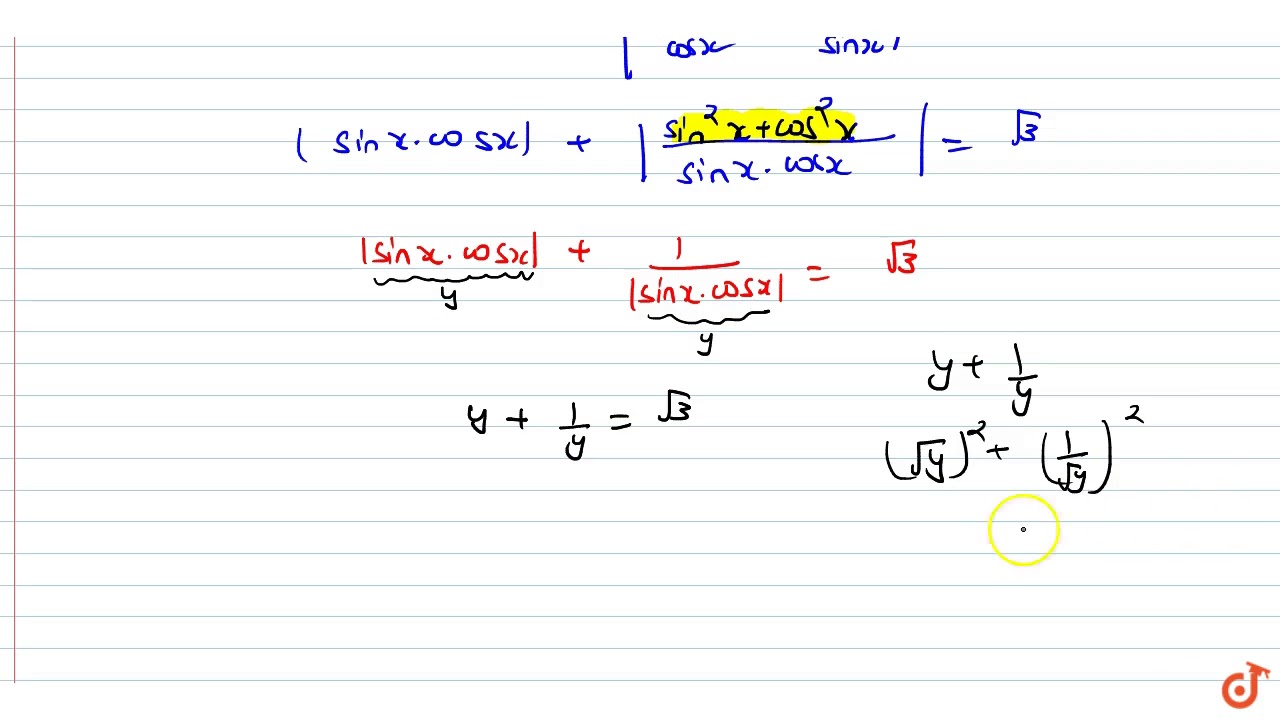


Number Of Roots Of The Equation Sinxcosx Sqrt 2 T A N 2x Cot 2x Sqrt 3 X In 0 4pi A R Youtube
\begin{align} f(y) = y^2 2 \\ 0 = y^2 2 \\ 2 = y^2 \\ y = \sqrt(2), \sqrt(2) \end{align} The following graph represents the area we intend to find WeFeb 01, 12 · the trouble lies with the √ symbol in the real numbers, we can enforce a definition that turns √ into a function (ie, singlevalued) but this definition breaks down in the complex numbers why?To find the equation of a line you need a point and a slope;



Computer Algebra Recipes



Tan Joke Gifts Merchandise Redbubble
A heartfelt "Thank you" goes to The MathJax Consortium and the online Desmos Grapher for making the construction of graphs and this webpage fun and easyIntegrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;Yo mama so mean she has no standard deviation level 1 Comment deleted by user 7 years ago 1 child level 2 Haha thats funny!
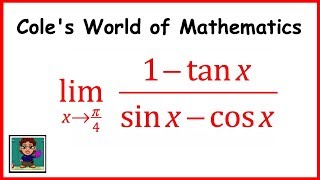


Limit Of 1 Tan X Sin X Cos X Calculus 1 Trig Limits Youtube



Misc Punpedia
42 votes, 14 comments 224k members in the mathpics communityProcess capability compares the output of an incontrol process to the specification limits by using capability indicesThe comparison is made by forming the ratio of the spread between the process specifications (the specification "width") to the spread of the process values, as measured by 6 process standard deviation units (the process "width")May 26, · Section 13 Trig Substitutions As we have done in the last couple of sections, let's start off with a couple of integrals that we should already be able to do with a standard substitution



10 Extra Cheesy Math Jokes Explained The Enotes Blog



Tan Joke Gifts Merchandise Redbubble
It is possible to simplify this Using the identity $\sin 2x=2\sin x\cos x$, we can write $\ds \sin 2u=2\sin u\cos u=2\sin(\arcsin x)\sqrt{1\sin^2 u}= 2x\sqrt{1\sin^2(\arcsin x)}=2x\sqrt{1x^2}$ Then the full antiderivative is $$ {\arcsin x\over2}{2x\sqrt{1x^2}\over4}= {\arcsin x\over2}{x\sqrt{1x^2}\over2}C $$Numberphile's channel on Youtube has a video about that!It is better to believe in men too rashly, and regret, than believe too meanly



Tlocv3cpsmjsgm


Short Jokes Dataset Thejokecafe Csv At Master Amoudgl Short Jokes Dataset Github
Dec 12, 17 · edit @DavidHammen has just posted a much more thorough and insightful answer, which also points out some problems applying Newton's method to the current form I'm pretty sure there are has never been an analytical expression discovered to solve $\nu(tt_p)$, but solving using Newton's method applied to $$ \sqrt{\frac{a^3}{\mu}}*(\arcsin(X) e*X) (tt_p) = 0 $$Jun 26, · Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation HistoryHow to integrate {eq}\sqrt{1cos(x)} {/eq} Integrals of Trigonometric Functions A common method used to evaluate integrals of trigonometric functions is substitution



Pin By Applequince On Geeky Me Math Humor Funny Math Jokes Funny Exam Answers



Tan Joke Gifts Merchandise Redbubble



Limit Of Sin X X As X Approaches 0 Video Khan Academy



Amazon Com I M Sec C And I Know It Funny Sexy Math Humor T Shirt Clothing


Physics Jokes Mardokay Mosazghi Brilliant



Tan Joke Gifts Merchandise Redbubble


Trig Insert Clever Math Pun Here


Chalk 21 04 02



Sqrt Stickers Redbubble



Lesson Reading Guide 2597 0k Mcgraw Hill Higher Education



Funny Short Math Jokes And Puns Math Is Fun
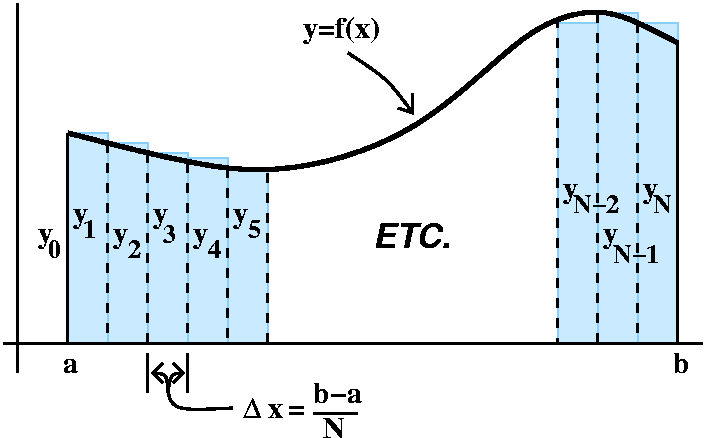


Diary Outline For Math 152h Fall 09



Proof That P Is Irrational Wikipedia



Maths Jokes


Cialis Side Affect Cialis Lowest Price Nerdytshirt Canadian Pharmacy Guaranteed Shipping



Math Math Jokes 4 Mathy Folks



900 Math Ideas In 21 Math Humor Math Jokes Math



What Is The Funniest Math Joke You Know Of Beakal Tiliksew Brilliant


Maths Jokes



Math Fun Todd Quinto S Website



The Academy Corner Dong Thap In South Vietnam Portal Manualzz



Circular Values Math And Statistics With C 11 Codeproject



Practice 3379 0k Mcgraw Hill Higher Education



10 Extra Cheesy Math Jokes Explained The Enotes Blog



Jokes Science Engineering And Math Jokes Mathematical Proof Teaching Mathematics
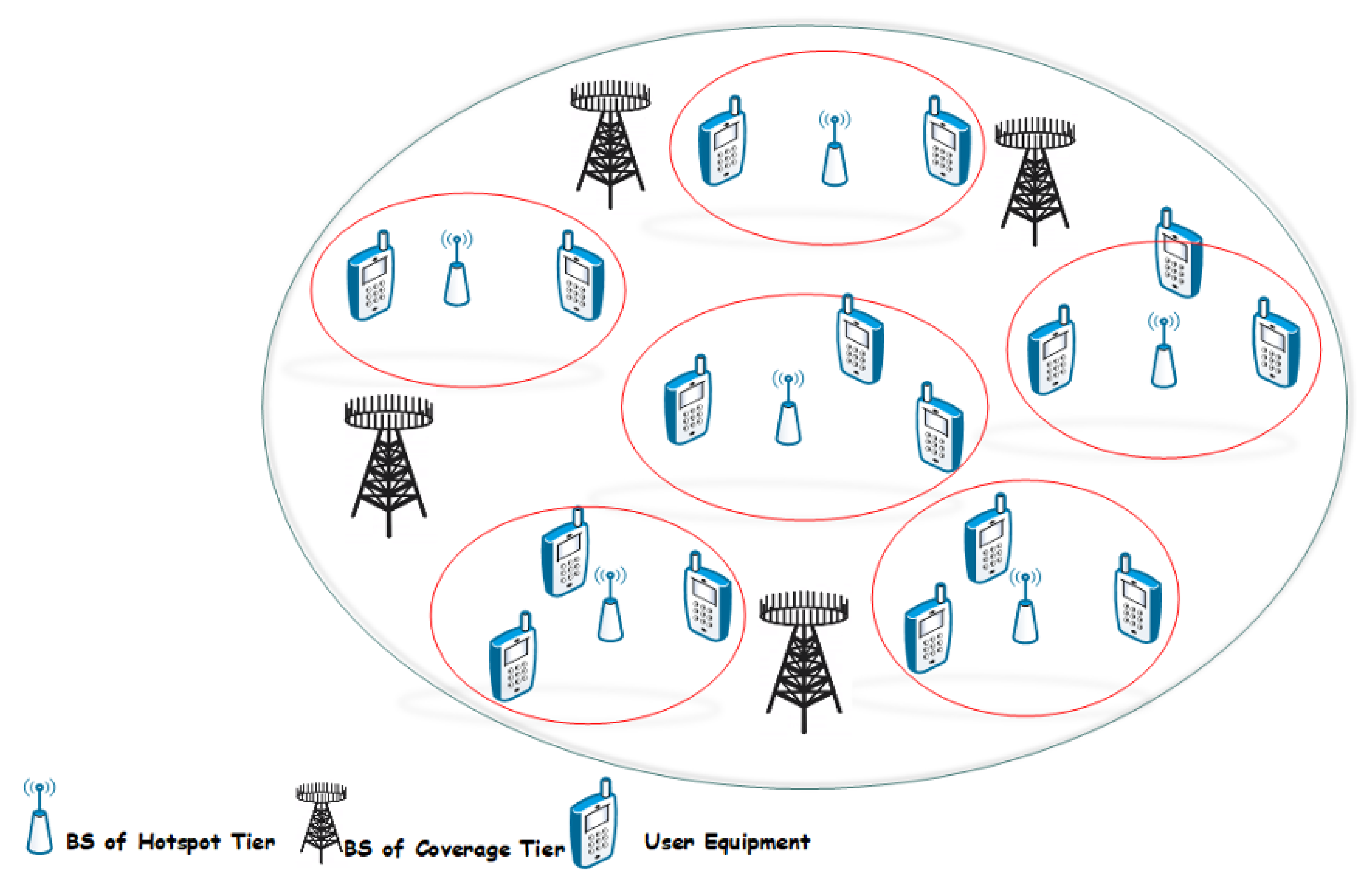


Sensors Free Full Text Spectral Efficiency Augmentation In Uplink Massive Mimo Systems By Increasing Transmit Power And Uniform Linear Array Gain Html


Molecules With Silly Or Unusual Names Page 4



If Tan 8 2 3 What Is Sin 8 Quora



If Tan 1 Sqrt 1 X 2 1 X Pi 45 Then Youtube



Spectacularly Nerdy Math Jokes Math Jokes Nerdy Jokes Math Humor



Algebra 2 Free Course By Tennessee School Boards Association On Itunes U



Short Sweet Math Challenges The Museum Of Hp Calculators



List Of Math Formulas



Math Fun Todd Quinto S Website


The Universe Of Discourse Category Math



View Question End Of Day Wrap



Math Fun Todd Quinto S Website



Bart Wronski Graphics Photography Machine Learning Image And Signal Processing



The Marquee Volume 34 Issue 2 By The Marquee Issuu


One Liner Joke Jokes Json At Master Faiyaz26 One Liner Joke Github



Math Fun Todd Quinto S Website



Mathematics Narinder



10 Extra Cheesy Math Jokes Explained The Enotes Blog


Trig Insert Clever Math Pun Here
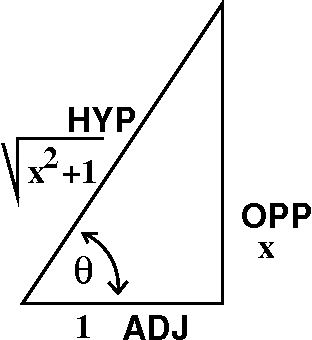


Diary Outline For Math 152h Fall 09



Funny Math Puns Jokes Mathpics



Last Day I M Sec C And I Know It I M 1 Tan2 C And I Know It Products


Epilogue Springerlink


D Y C O M A S Y The Dynamic Content Management System



Amazon Com I M Sec C And I Know It Funny Sexy Math Humor T Shirt Clothing



Pin On Calculus Lesson Ideas



Funny Short Math Jokes And Puns Math Is Fun



Math Fun Todd Quinto S Website



Math Is Useful Translation I M Sec C And I Know It Math Puns Math Jokes Math Humor


Integral Tan 5 X Sec 3 X Youtube


Molecules With Silly Or Unusual Names Page 4


Integral Of 1 Sqrt 1 X 2 Sin 1x Calculus Youtube



Stream 1 Number Systems Springerlink



Graph Math Jokes 4 Mathy Folks


What Does N Mean Quora



Pre Calculus Math Love


Diary Outline For Math 152h Fall 09



10 Extra Cheesy Math Jokes Explained The Enotes Blog


Molecules With Silly Or Unusual Names Page 4



What Are Some Funny Mathematics Jokes Quora



0 件のコメント:
コメントを投稿