x³y³=(X+Y)(X²-XY+Y²) xy=1 x³y³=X²-XY+Y² x3y33xy=X²2XY+Y²=(xy)²=1Near (x, y)=(3245, 197), (309, 845), (25, 9) and (2365, 15) And since the two equations can be combined into a quartic in x, (or a quartic in y) and a quartic has 4 roots in the complex numbers and we have found 4 real roots then these are the only solutions even if you allowed x and y to be complex numbers (x y z) 2 = x 2 y 2 z 2 2xy 2yz 2zx (x y) 3 = x 3 y 3 3xy(x y) (x – y) 3 = x 3 – y 3 – 3xy(x – y) x 3 y 3 z 3 – 3xyz = (x y z)(x 2 y 2 z 2 – xy – yz – zx;
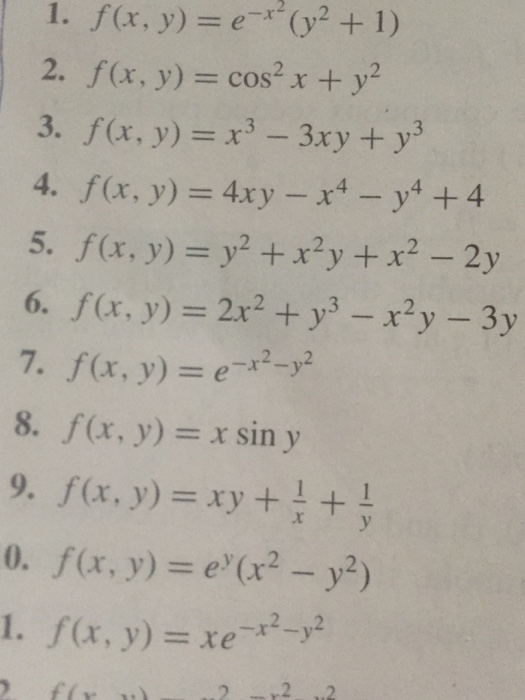
F X Y E X 2 Y 2 1 F X Y Cos 2 X Y 2 Chegg Com
(x+y)^3=x^3+y^3+3xy(x+y)
(x+y)^3=x^3+y^3+3xy(x+y)-1 How do you simplify the cube of a binomial?Telangana SCERT Class 9 Math Chapter 2 Polynomials and Factorisation Exercise 25 Math Problems and Solution Here in this Post Telanagana SCERT Class 9 Math Solution Chapter 2 Polynomials and Factorisation Exercise 25
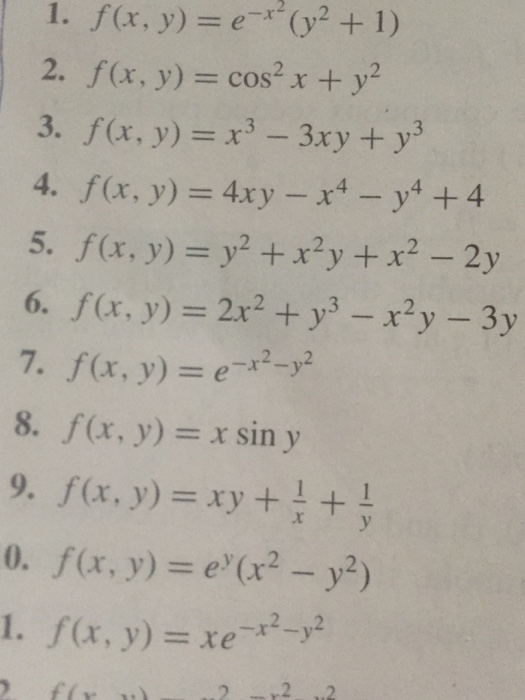



F X Y E X 2 Y 2 1 F X Y Cos 2 X Y 2 Chegg Com
If x y = 12, and xy = 27, then find the value of x3 y3 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries If xy = 4 and xy = 21 then find the value of x3 y3 Maths Polynomials NCERT Solutions;(x y) 3 = x 3 y 3 3xy(x y) (x – y) 3 = x 3 – y 3 – 3xy(x – y) x 3 y 3 z 3 – 3xyz = (x y z) (x 2 y 2 z 2 – xy – yz – zx) Share these Notes with your friends Prev Next > You can check our 5step learning process Classes Class 6 Class 7 Class 8 Class 9 Class 10 Class 11 Class 12 NEET Subjects Physics
(i) x 3 y 3 = (x y)(x 2 – xy y 2) (ii) x 3 – y 3 = (x – y) (x 2 xy y 2) Solution (i) We know that, (x y) 3 = x 3 y 3 3xy (x y) ⇒ x3 y3 = (x y)3 – 3xy (x y) = (x y) (x y) 2 – 3xy = (x y) x 2 y 2 2xy – 3xy = (x y) x 2 y 2 – xy = RHS Hence proved, (ii) We know that, (x – y) 3 = x 3 – y 3 – 3xy (x – y) x 3 – y 3Philip Macdonald Answered 1 year ago Author has 234 answers and 413K answer views xy =7, xy =1 (xy)^3 = x^3 3x^2*y 3x*y^2 y^3 = x^3y^3 3xy (xy) Then 7^3 = x^3y^3 3*1*7, ie, x^3y^3 = 7^3 7*3 = 7 (7^2 3) = 7*46 =322 143 views Sponsored by Jumbo Privacy & Security = (4a – 3b) 3 ∵ (x – y) 3 = x 3 – y 3 – 3xy(x – y) = (40 – 3b) (4a – 3b) (4a – 3b) Question 3 What are the possible expressions for the dimensions of a cuboid whose volume is given below ?
0 Follow 0 A K Daya Sir, added an answer, on 25/9/13 A K Daya Sir answered this x 3 y 3 = (x y) (x 2 xy y 2 ) this formula can be derived from (x y) 3 = x 3 y 3 3xy (x y) x 3 y 3 = (x y) 3 3xy (x y) x 3 y 3 = (x y) (x y) 2 3xy = (x y) x 2 y 2 2xy 3xy = (x y) (x 2 xy y 2 ) Was this answer helpful?X 0 =1 x a y a = (xy) a, 2 2 3 2 = 6 2;Kuchaman Maths Guru !



Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community




Let F X Y X 3 3x 2y 3 2y 2 We Find Fx X Y 3x 2 Chegg Com
= x^3 3x^2y 3xy^2 y^3 = x^3 y^3 3xy(x y) Also, Read Cube of a Binomial Cube of Sum of Two Binomials Examples 1 Determine the expansion of (x 2y)^3 Solution The given expression is (x 2y)^3 We have an equation on cubes like (x y)^3 = x^3 y^3 3xy(x y) By comparing the above expression with the (x y)^3 Here, x2y=2 y=1 Hence, putting the value of y again in any of the above three equations will give the value of x So, taking equation x=y5 x=1–5 x=4 So the final answers are x=4 and y=1 For any clarification, please update in comments And if you liked the answer do upvote and sorry for any grammatical mistakes35 (1) Upvote (1) Choose An Option That Best Describes Your Problem Answer not in Detail Incomplete Answer Answer Incorrect Others Answer not in Detail Incomplete Answer Answer Incorrect
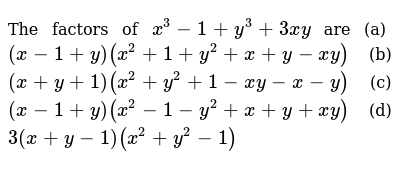



The Factors Of X 3 1 Y 3 3x Y Are A X 1 Y X 2 1 Y 2 X Y
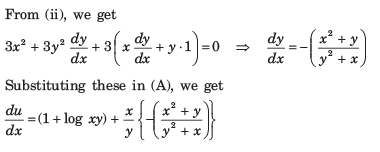



If U X Log Xy Wherex3 Y3 3xy 1 Then Du Dx Is Equal Toa B C D Correct Answer Is Option A Can You Explain This Answer Edurev Electronics And Communication Engineering Ece
Ĺet x^yy^x=(xy)^3=x^3y^33xy(xy) Or,x^yy^x=x^3y^39xy again x=3y so x^3y^39xy=(3y)^3y^39(3y)y=2727y9y^2y^3y^39y^227=5427y Now we got 54 27y=27, or 27y=27,y=1 Then x=31=2 The values of x& y only satisfy xy=3 and doen't satisfy x^yy^x=27 So there is no solution for the values of x & y Answer (xy)^3 = (xy)^2 (xy) = (x^2y^22xy) (xy) = x^3xy^22x^2yx^2yy^32xy^2 = x^3y^33x^2Without doing the maths the answer is very clearly yes!
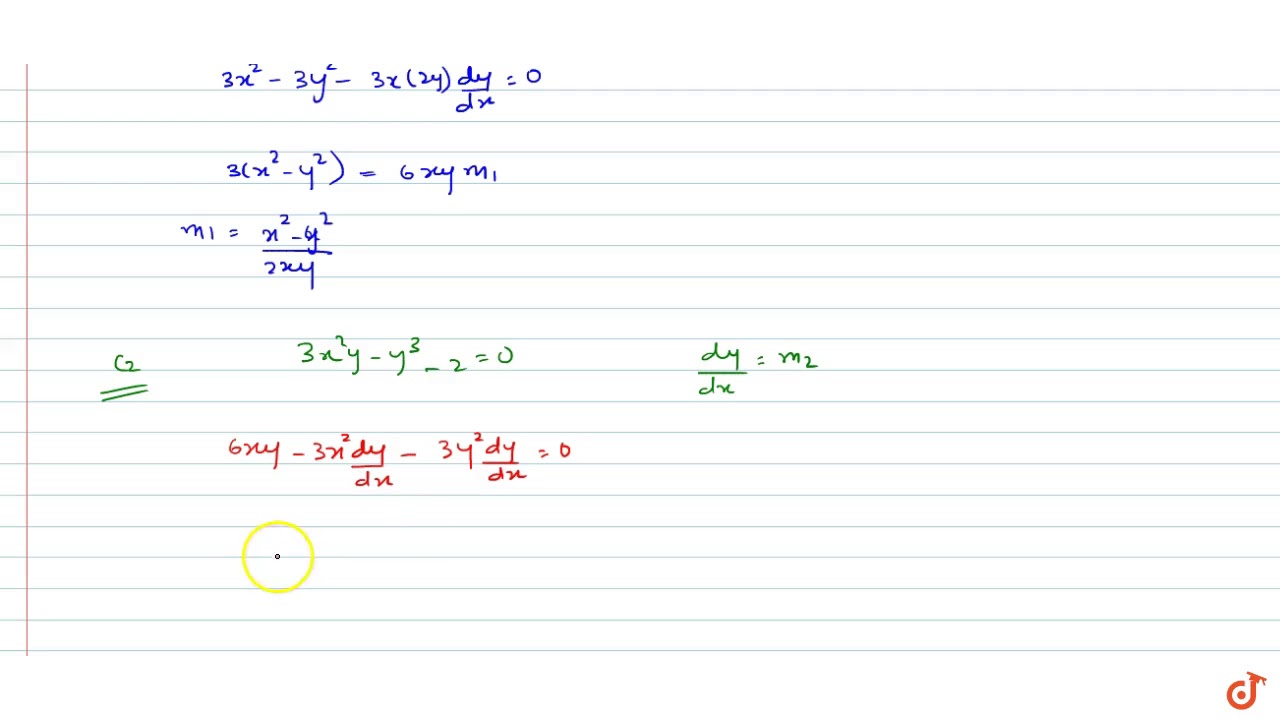



The Two Curves X 3 3xy 2 2 0 And 3x 2y Y 3 2 0 Youtube




If X 3 Y 2 3xy X Y Then Log X Y 3
Start your 48hour free trial to unlock this answer and thousands more Enjoy eNotes adfree and cancel anytimeTutor Contact tutor 7 months ago Use identity ( a b)^3 = a^3 b^3 3ab (a b ) Put a= x and b= y ( x y)^3 = x^3 y^3 3xy ( x y ) In further step 3xy can be multiplied inside the bracket The answer is 👍 HelpfulVolume = 12ky 2 8ky – k Solution We have, volume = 12ky 2 8ky – k = 4k(3y 2 2y – 5) = 4k(3y 2 5y – 3y – 5)




X 9y 3xy X Y Answer It Plz With Full Maths Brainly In




If X Y 1 Then Find The Value Of X3 Y3 3xy Brainly In
In mathematics, the cube of sum of two terms is expressed as the cube of binomial x y It is read as x plus y whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ( x y) 3 = x 3 y 3 3 x 2 y 3 x y 2Ĺet x^yy^x= (xy)^3=x^3y^33xy (xy) Or,x^yy^x=x^3y^39xy again x=3y so x^3y^39xy= (3y)^3y^39 (3y)y=2727y9y^2y^3y^39y^227=5427y Now we got 54 27y=27, or 27y=27,y=1 Then x=31=2 The values of x& y only satisfy xy=3 and doen't satisfy x^yy^x=27 So there is no solution for the values of x & yThere are two variables and one equation so there will be an infinite number of solutions Let's solve for y xy = xy x = xy y factor out the y x = y (x1) x x − 1 = y so y = x x − 1 x ≠ 1



F X Y E X 2 Y 2 1 F X Y Cos 2 X Y 2 Chegg Com
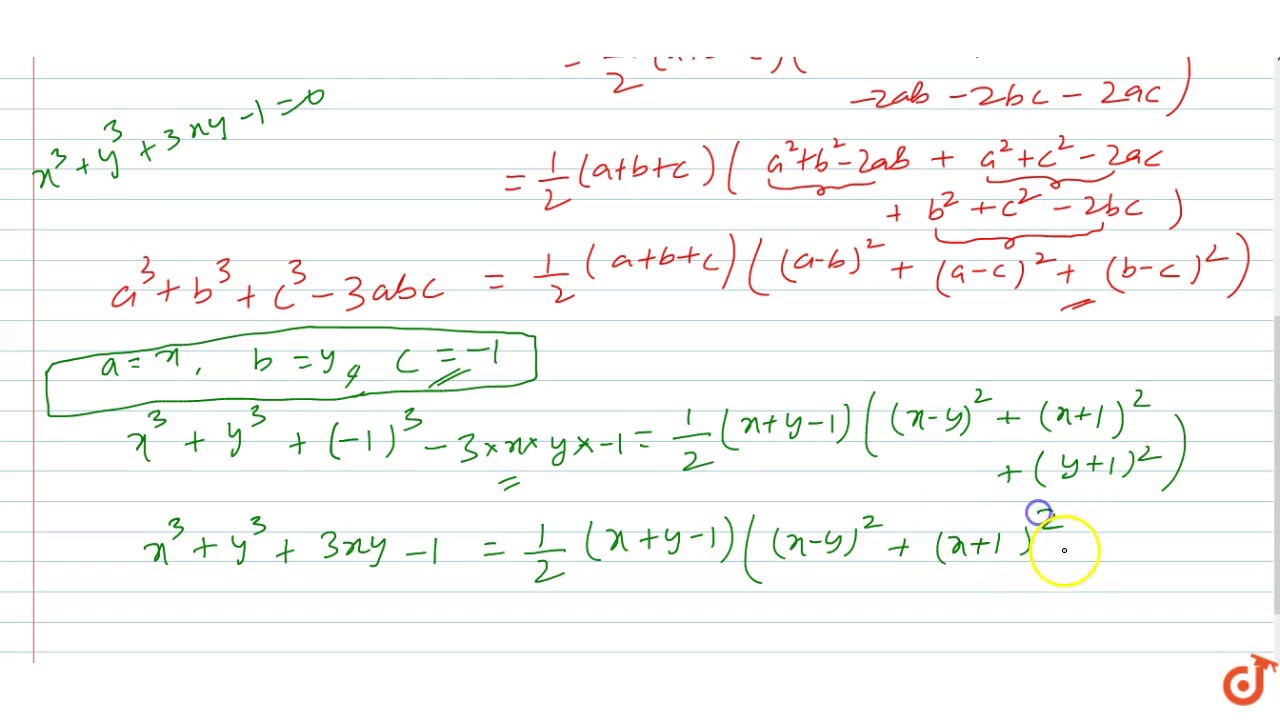



Q 16 Locus All Point P X Y Satisfying X 3 Y 3 3xy 1 Consists Of Union Of A A Youtube
#(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2# Always expand each term in the bracket by all the other terms in the other brackets, but never multiply two or more terms in the same bracketWe know that (x y) 3 = x 3 y 3 3xy (x y) Using Identity VII ⇒ x 3 y 3 = (x y) 3 3xy (x y) x 3 y 3 = (x y) { (x y) 2 3xy} ⇒ x 3 y 3 = (x y) (x 2 2xy y 2 3ry) Using Identity IV ⇒ x 3 y 3 = (x y) (x 2 xy y 2 ) 350 ViewsSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



1




Let F X Y X 3 3xy 2 2y 3 Show That The Chegg Com
State reasons for your answer Ans (i) 4x 2 – 3x 7 ⇒ 4x2 – 3x 7x° ∵ All the exponents of x are whole numbers ∴ 4x 2 – 3x 7 is a polynomial in one variable (ii) ∵ All the exponents of y Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given (i) Area 25a2 – 35a 12 (ii) Area 35y2 13y – 12 Solution (i) We have, area of rectangle = 25a 2 – 35a12 = 25a 2 – a – 15a12 Using formula, (x – y) 3 = x 3 – y 3 – 3xy(x – y) (99) 3 = (100 – 1) 3 = (100) 3 – 1 3 – (3 × 100 × 1) (100 – 1) = – 1 – 300(100 – 1



If X Y 2 Then What Is The Value Of X Y 6xy Quora




If X 3 Y 2 3xy X Y Then Log X Y 3
X 3 y 3 3xy = 1Maths Tutor Chandigarh, Chandigarh, India 486 likes 7 talking about this My self Sujit Adhikari from Chandigarh If you need Mathematics teacher, please feel free to contact me atLogin Create Account (xy) 3 = x 3y 3 3xy(xy)(4) 3 =x 3y 3 3(21)464=x3y3252x 3y 3 =x 3y 3 =1 0




If X Y 7 And X3 Y3 133 Find I Xyii X Y Brainly In




Transform X 3 Y 3 3xy 0 Mathematics Stack Exchange
The algebraic identities for class 9 consist of identities of all the algebraic formulas and expressions You must have learned algebra formulas for class 9, which are mathematical rule expressed in symbols but the algebraic identities represent that the equation is true for all the values of the variables For example;The formula is (xy)³=x³y³3xy(xy) Proof for this formula step by step =(xy)³ =(xy)(xy)(xy) ={(xy)(xy)}(xy) =(x²xyxyy²)(xy) =(xy)(x²y²2xy) =x³xy²2x²yyx²y³2xy² =x³y³3x²y3xy² =x³y³3xy(xy) Hence proved also!So we set it = 0 i*sqrt(3)(x1) = 0 x1 = 0 x = 1 Then substituting that y = y = y = y = 1 So we end up with all solutions {(x,y) x y = 1} plus the one solution (x,y) = (1,1) Now if you were asking about xy instead of xy, the answer would be xy is always either 1 or 2 Are you sure you didn't make a typo and you were asking about xy and not xy?




Analyze The Product Of X 3 9y 3 3xy X Y




Second Partials Test For F X Y X 3 3xy Y 3 Youtube
5 Linear Polynomial A polynomial of degree one is called a linear polynomial eg, x √7 is a linear polynomial in x, y and z √2 µ 3 is a linear polynomial in µ 6 Quadratic Polynomial A polynomial of degree two is called a quadratic polynomial eg;(xy) 3 = x 3 y 3 3xy(x y) x 2 y 2 = (x y)(x y) x2 = 1/x 2, 24 = 1/16 = 1/2 4 (x a)(x b) = x ab;Make Easy Maths,Math Shortcuts,math magic tricks,learn math,vedic maths tricks,easy maths,maths tricks in hindi,number tricks,maths online,maths for fast calculation



Find The Extreme Values Of The Function X 3 Y 3 3xy Sarthaks Econnect Largest Online Education Community




If X 3 Y 3 3xy 2 3x 2y 1 0 Then At 0 1 Dy Dx
It is clear that when $x=y$ we have $x^3y^3=0$ Then use long division to divide $x^3y^3$ by $xy$ and the result will be the equation on the right Another way would be to write $$\left(\frac{x}{y}\right)^3 1$$ Now we wish to find the zeros of this polynomial 4 It's two equations, with two variables We can do what we always do You can write y = 8 / x, and substitute into the first equation, obtaining x3 / x3 = 72 From here, we want to write this as a polynomial, so we multiply through x3 so there are no negative powers, and then move everything to the left1 Explanation We know that algebraic formula, (x y) 3 = x 3 y 3 3xy (x y) put the value of x y in given equation given, x y = 1 1 = x 3 y 3 3xy X 1?




Find Dydx Where X 3 Y 3 3xy 7




Find X3 Y3 3xy If X Y 1 Brainly In
Get FREE NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 25 We have created Step by Step solutions for Class 9 maths to help you to revise1 Which of the following expressions are polynomials in one variable and which are not?(X – Y) 3 = X 3 – Y 3 – 3XY(X – Y) Or (X – Y) 3 = X 3 – Y 3 – 3X 2 Y 3XY 2 Was this answer helpful?




Najdite Znachenie Vyrazheniya X Y X 2 Xy Y 2 3xy X 3 Y 3 1 X Y Pri X 2 1 Y 0 Shkolnye Znaniya Com




Verify X Y 3 X3 Y3 3xy X Y Brainly In
Solve for x Use the distributive property to multiply xy by x^ {2}xyy^ {2} and combine like terms Use the distributive property to multiply x y by x 2 − x y y 2 and combine like terms Subtract x^ {3} from both sides Subtract x 3 from both sides Combine x^ {3} and x^ {3} to get 0 Combine x 3 and − x 3 to get 0 (x y) 3 = x 3 3x 2 y 3xy 2 y 3 = x 3 y 3 3xy(x y) So 9 3 = x 3 y 3 3*10*9 x 3 y 3 = 729 270 = 459 Alan(x y)^3 = (x^3) (y^3) 3xy(x y) so, (3)^3 = 9 3xy(3) so, 27 = 9 9xy so, (27 9)/9 = xy so, xy = 18/9 = 2




Prove X Y 3 X 3 Y 3 3xy X Y Brainly In
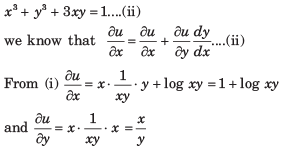



If U X Log Xy Wherex3 Y3 3xy 1 Then Du Dx Is Equal Toa B C D Correct Answer Is Option A Can You Explain This Answer Edurev Electronics And Communication Engineering Ece
Solution (By Examveda Team) Given, xy = 2 cubing both sides (xy) 3 = 2 3 => x 3 y 3 3xy ( xy) = 8 => x 3 y 3 3×15×2= 8 => x 3 y 3 90 = 8 => x 3 y 3 = 0If xy = 7 and xy = 10, then (xy)^3 = x^33x^2y3xy^2y^3 = x^3y^3 3xy(xy), or 7^3 = x^3y^3 3*7*10, or x^3y^3 = 343–210 = 133 So, x^3y^3 = 133Cube of a binomial can be simplified using the identities \({(x y)}^3 = x^3 y^3 3xy(x y)\)




If X 3 Y 3 1 3xy Where X Y Determine The Value Of X Y 1




X Y 3 X 3 Y 3 3xy X Y Verify Maths Meritnation Com
X a /x b = x ab = 1/x ba;Polynomial Examples Find the remainder when x 4 x 3 – 2x 2 x 1 is divided by x – 1 Solution Here, p(x) = x 4 x 3 – 2x 2 x(x1) (x2) = x 2 3x 2



How To Solve X 3 3xy 2 Dx 3x 2y Y 3 Dy Quora




Solve X 3 2y 3 Dx 3xy 2dy 0
xy=3 xy=3 Recall the cubic formula (xy)^3=x^3y^33xy(xy) Substitute the required values 3^3=x^3y^33*3(3) 27=x^3y^327 x^3y^3=0Xy yz zx is a quadratic polynomial in x, y and zQuadratic equation, for any given x if ax 2 bx c =0 then x has 2 solutions x=(b√(b 2 4ac)/2a, x=(b√(b 2 4ac)/2a x a y b is not equal to (xy) ab




Issledovat Na Ekstremum Funkciyu Dvuh Peremennyh Z F X Y Z X 3 Y 3 3xy Shkolnye Znaniya Com



1
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history • (x – y) 3 = x 3 – y 3 – 3xy(x – y) • x 3 y 3 z 3 – 3xyz = (x y z)(x 2 y 2 z 2 – xy – yz – zx) Also, check the NCERT Solutions for Class 9 Maths Chapter 2 from theReport this is not the correct method to do the exercise Log into add a comment kvnmurty X y = 12 xy = 27 (xy)^3 = x^3y^3 3xy (xy) x^3 y^3 = (xy)^3 3 xy (xy) = 12^3 3 * 27 * 12




X X 3 Y 3 3xy X Y




न म न व य जक क ग णनखण ड क ज य X X 3 Y 3 3xy X Y Youtube
We know that algebraic formula, (x y) 3 = x 3 y 3 3xy (x y) put the value of x y in given equation given, x y = 1 1 = x 3 y 3 3xy X 1 ⇒ x 3 y 3 3xy = 1 Previous Question Next Question Your comments will be displayed only after



If X 3 Y 3 9 And X Y 3 Then The Value Of X 4 Y 4 Please Answer Honestly Don T Watch Others Quora



Search Q X Y 5e3 Expand Formula Tbm Isch



If Math X 3 Y 3 3xy 1 Math What Is The Minimum Value Of Math X 2 Y 2 Math Quora



If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9




X X 3 Y 3 3xy X Y




If X Y 7 And X 3 Y 3 133 Find X 2 Y 2 Brainly In




Factorise X3 9y3 3xy X Y Brainly In
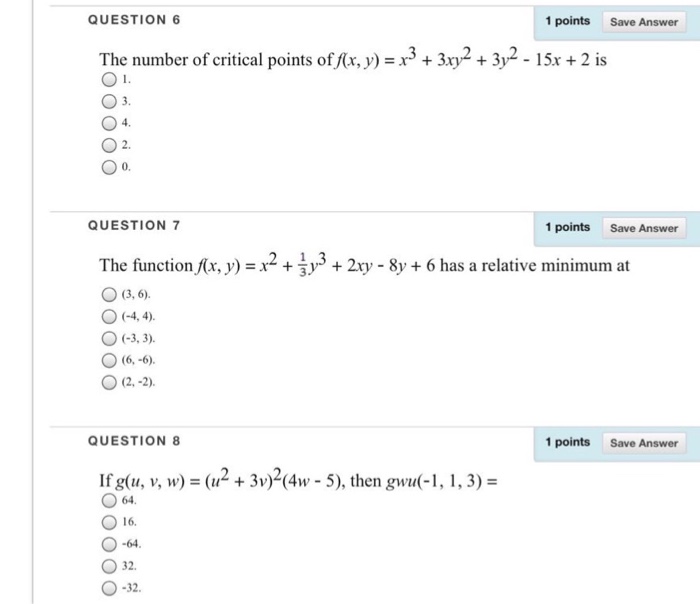



The Number Of Critical Points Of F X Y X 3 Chegg Com




What Are The Factors Of X Y 3 X3 Y3 Brainly In



Search Q X3 2b Y3 2b Z3 Tbm Isch




If X 3 3xy 2y 3 17 Then In Terms Of X And Y Chegg Com




Prove That X Y 3 X Y 3 6y X 2 Y 2 8y 3 Mathematics Topperlearning Com Jd2kccrr




Uprostite Vyrazhenie A X 2 Y 2 3xy 3y X Y B S 2 49 10cd 2c 14 5d V X 2 10x 25 3x 12 2x 10 X 2 16 G T 3 8 12t 2 27t 4t 9 T 2 2t 4




Cho X Y 1 Tinh Gia Trị Của Biểu Thức X 3 Y 3 3xy Cho X Y 1 Tinh Gia Trị Của Biểu Thức X 3 Y 3




Find The Critical Points Of F X Y X 3 Y 3 3xy Chegg Com




Ppt Polynomials Powerpoint Presentation Free Download Id




Prove That X2 Y2 C X2 Y2 2 Is The General Solution Of The Differential Equation X3 3xy2 Dx Y3 3x2y Dy Where C Is Parameter Mathematics Shaalaa Com



Solve X 3 3xy 2 Dx Y 3 3x 2y Dy Sarthaks Econnect Largest Online Education Community




Find All Values Of X Y Where Theorem 3 1 1 The Chegg Com




X Y Xy 3x 3y 12 A Arătați Ca X Y X 3 Y 3 3 B Arătați Ca X 3 3 X Brainly Ro




X Y 3 X3 Y3 3xy X Y Brainly In



The Two Curves X 3 3xy 2 2 0 And 3x 2y Y 3 2 0 Intersect At An Angle Of Sarthaks Econnect Largest Online Education Community




X X3 Y3 3xy X Y Brainly In




Ex 2 5 9 Verify I X3 Y3 X Y X2 Xy Y2 Ex 2 5




X X3 Y3 3xy X Y Maths Polynomials Meritnation Com



Locus Of All Point P X Y Satisfying X 3 Y 3 3xy 1 Consists Of Union Of Sarthaks Econnect Largest Online Education Community
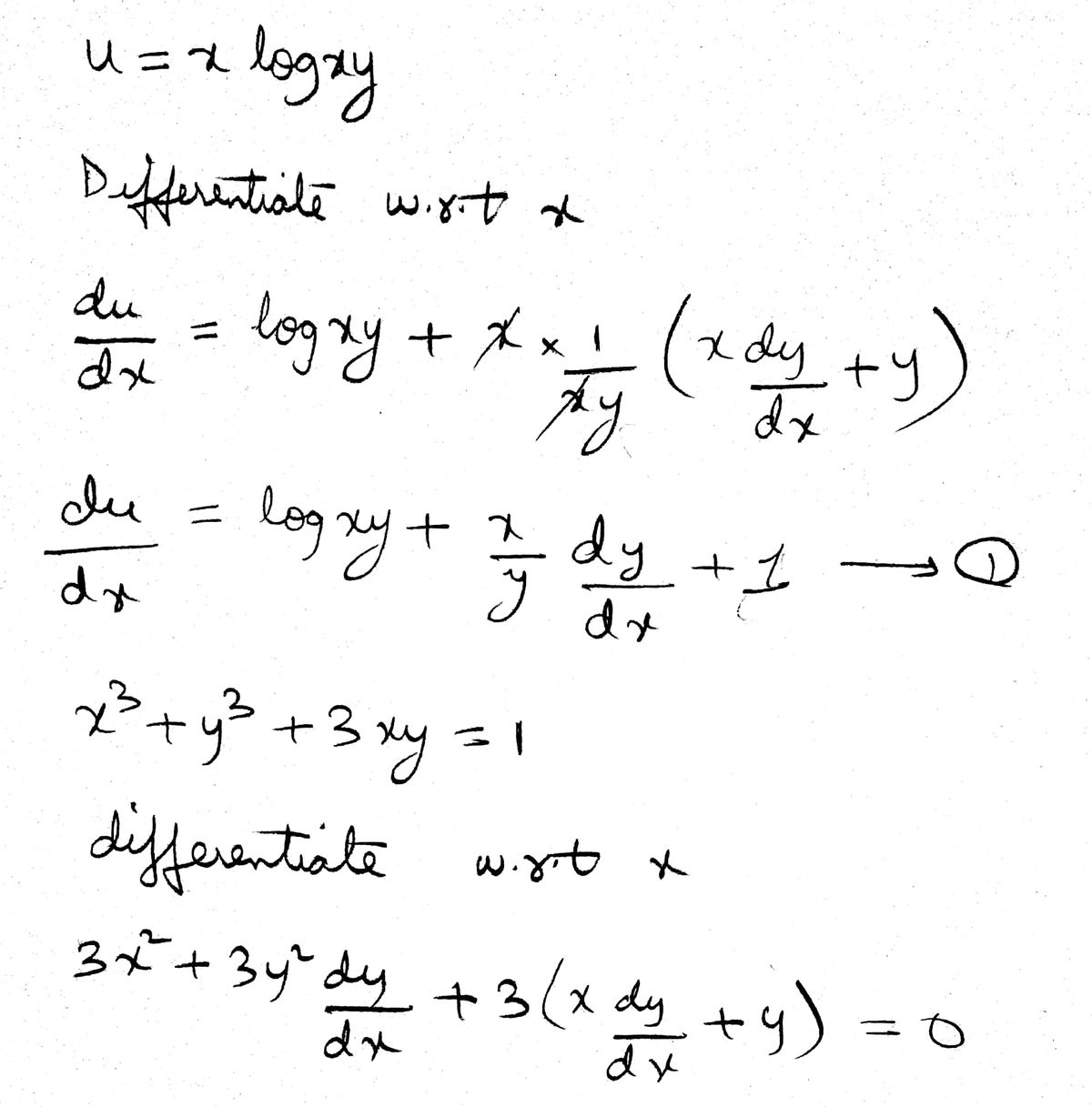



Answered If U X Log Xy Where X3 Y3 3xy 1 Find Bartleby




Tinh Gia Trị Biểu Thức A X 3 3xy X Y Y 3 X 2 2xy Y 2 Khi X Y 7 Cau Hỏi Hoidap247 Com
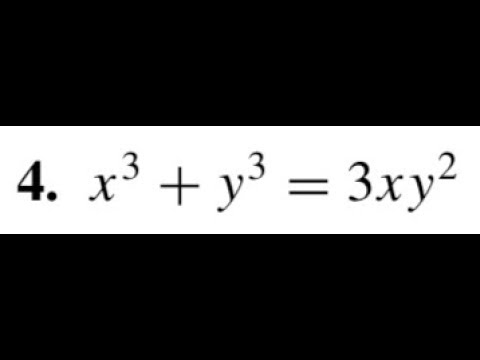



X 3 Y 3 3xy 2 Find Dy Dx Using Implicit Differentiation Youtube
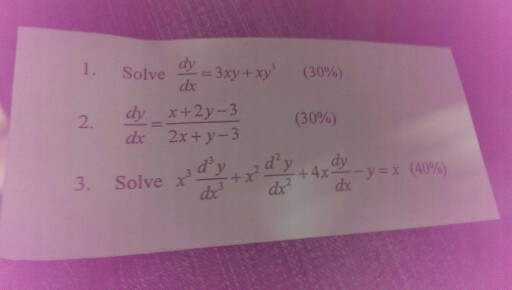



Solve Dy Dx 3xy Xy 3 30 Dy Dx X 2y 3 2x Chegg Com



Maximum Value Of The Function F X Y X 3 Y 3 3xy Is Sarthaks Econnect Largest Online Education Community




If X Y 1 Then Find The Value Of X 3 Y 3 3xy Maths Continuity And Differentiability Meritnation Com
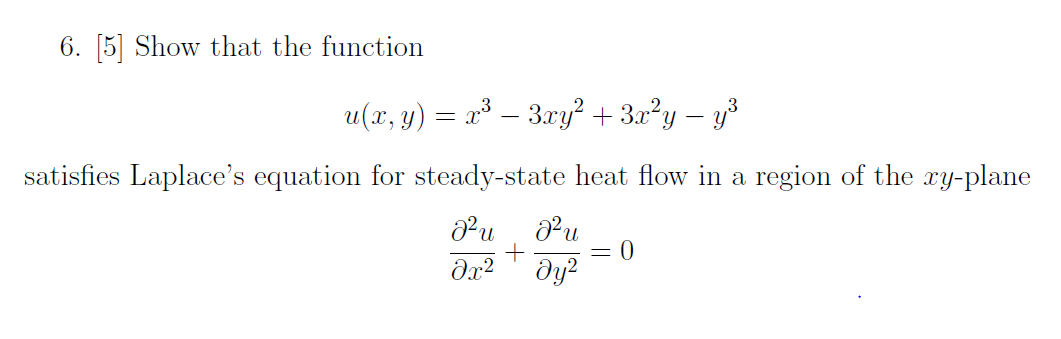



Show That The Function U X Y X 3 3xy 2 3x 2y Chegg Com




Factorise X Y 3 X 3 Y 3 3xy X Y Brainly In




Find Dy Dx By Implicit Differentiation X 2 Y 2 Chegg Com




How To Solve Math X 3 Y 3 Dx 3xy 2dy 0 Quora




Cau Hỏi Của Huỳnh Ngọc Nhien Toan Lớp 8 Học Trực Tuyến Olm
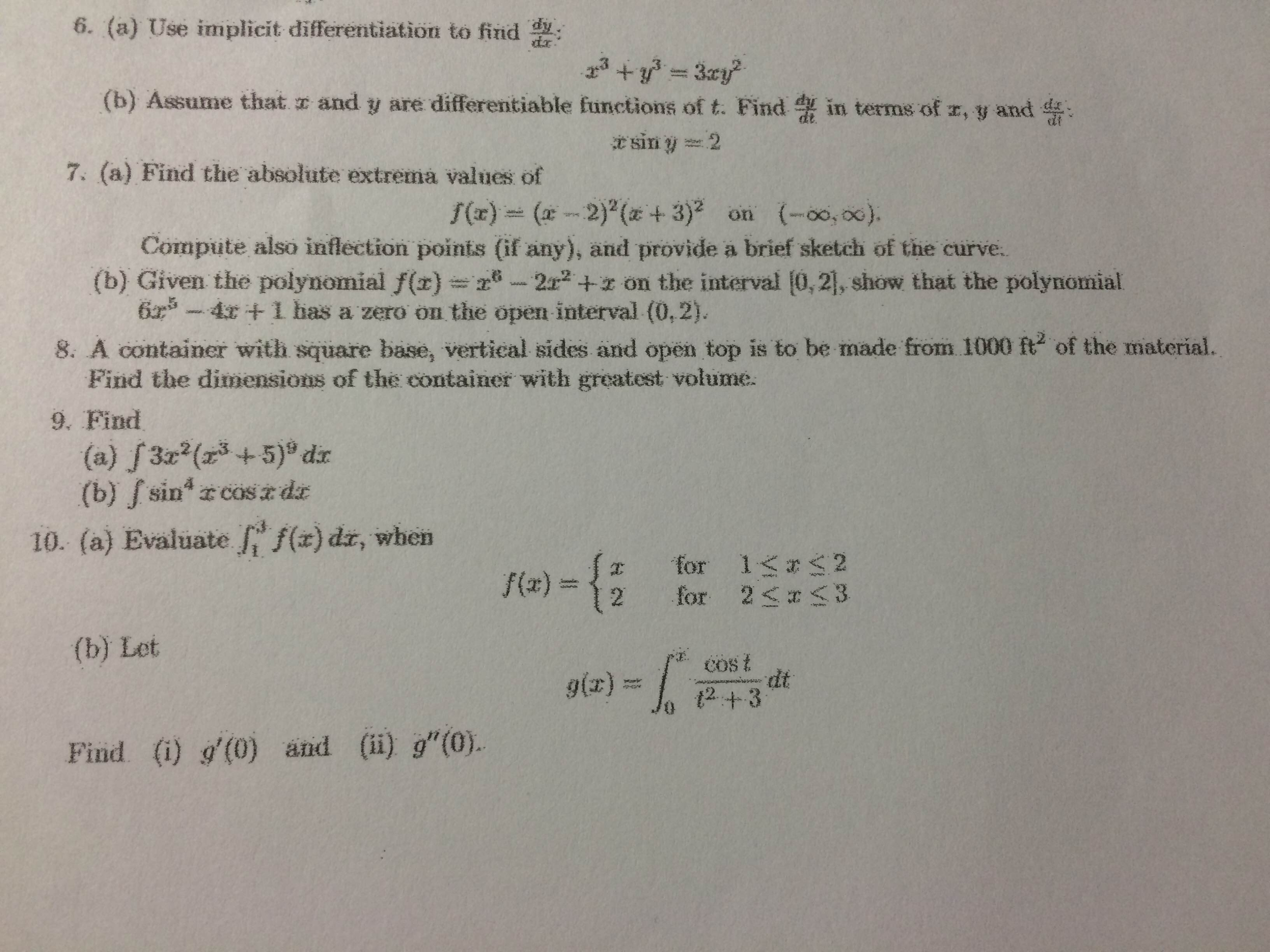



6 A Use Implicit Differentiation To Find Dy Dx Chegg Com




X 9y 3xy X Y Answer It Plz With Full Maths Brainly In




Consider The Function F X Y X 3 Y 3 3xy Chegg Com




Factorise X3 9y3 3xy X Y Brainly In




Factorise X X3 Y3 3xy X Y Brainly In




X Y 3 X3 Y3 3xy X Y Proof It Maths Polynomials Meritnation Com




Factorise X3 9y3 3xy X Y Brainly In




X 3 3xy Y 3 1 Slozhit Na Mnozhiteli Shkolnye Znaniya Com




Expand X X Y 3 3xy X Y




K 6y Y 1 7y 7y Jndei M 3x 4x N 6x X Je Gauthmath




If X 3 3xy 2 14 Y 3 3yx 2 13 And X Y Are Real Find The Maths Polynomials Meritnation Com




If X 3 Y 2 3xy X Y Then Log X Y 3



How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Dokazhite Tozhdestvo Tex Frac X 3 Y 3 X Y 2 Frac 3xy 2 Y 3 Shkolnye Znaniya Com




X 3 3xy 2 Dx Y 3 3x 2y Dy Youtube




Ppt Polynomials Powerpoint Presentation Free Download Id




Factories X3 9y3 3xy X Y Brainly In



How To Draw The Graph Of X 3 Y 3 3xy Quora




How To Solve Math X 3 Y 3 Dx 3xy 2dy 0 Quora




How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Factorise X X Y 3xy X Y Brainly In




Solve Differential Equation X 3 3xy 2 Dx Y 3 3x 2y Dy Maths Differential Equations Meritnation Com




Which Of The Following Is A Factor Of X Y 3 X 3 Y 3
.png)



X X3 Y3 3xy X Y Maths Polynomials Meritnation Com




Proof Of Formulae I X Y 3 X 3 Y 3 3xy X Y Ii X 3
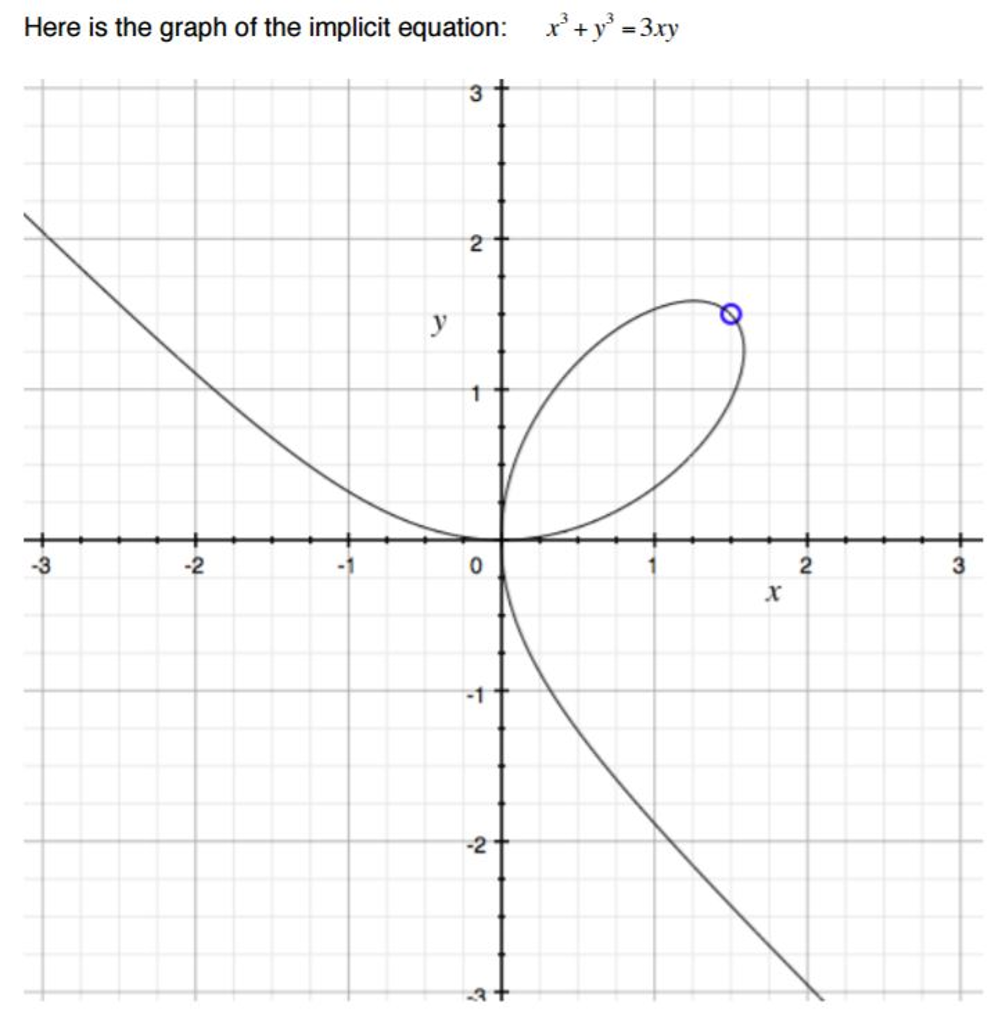



Here Is The Graph Of The Implicit Equation X 3 Y 3 Chegg Com




Factorise X X 3 3 3x 2y X Y Brainly In




The Factors Of X 3 1 Y 3 3x Y Are A X 1 Y X 2 1 Y 2 X Y




X 3 3x 2 X 3 Factorise Novocom Top




Y3 3xy2 X3 3x2y Find Dy Dx Plzzzzzzzzzzz Slove Ths As Fast As Possible Maths Continuity And Differentiability Meritnation Com




X3 9y3 3xy X Y এর উৎপ দক ব শ ল ষণ কর Brainly In




X Y 3 X3 Y3 3xy X Y Brainly In




How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com



0 件のコメント:
コメントを投稿